ARCHIV

Šachové myšlení (3) - alfabeta

Existuje algoritmus, který je mnohem rychlejší než minimax, protože některé varianty vůbec nepropočítává. Přesto dojde vždy ke stejnému výsledku. Tento zázračný algoritmus se jmenuje alfabeta metoda a je základem dnešních šachových programů.

12.5.2006 06:00 | Jan Němec | Články autora | přečteno 20098×

Alfabeta metoda

V minulém dílu jsme si ukázali algoritmus minimax, který, zhruba řečeno, počítá všechny tahy, všechny odpovědi na tyto tahy, všechny odpovědi na odpovědi a tak dále až do nějaké dané hloubky nebo do konce partie. Zároveň jsme si ukázali, že algoritmus není paměťově náročný, dnešní počítače mají dost paměti na to, aby prošly celý strom hry šachy. Přirozená otázka je, zda mají také dostatečnou trvanlivost, jinými slovy, kdy tento propočet skončí. Předpokládejme, že z pozice máme vždy 38 tahů a že dokážeme spočítat milión ohodnocovacích funkcí za vteřinu. Čas na provádění a generování tahů a další režii zanedbáme. Při úplném propočtu do hloubky n nás čeká 38ⁿ ohodnocovací funkcí. 38⁴ je asi 2 miliony, tady propočet do hloubky 4 půltahy neboli 2 tahy trvá 2 vteřiny. Hloubka 2 a půl tahu by už zabrala přes minutu. Propočet do hloubky 3 tahy by už program nezvládal ani při turnajovém tempu pro vážné partie. Při hloubce 20 tahů by myšlení trvalo přes 10⁵⁰ let, což není příliš uspokojivý výsledek.

Je zřejmé, že propočet do hloubky dvou tahů nemůže stačit na velmistry. Naopak úplné začátečníky, kteří se právě naučili pravidla, by měl program bez problémů porážet. Bude však stačit na běžné klubové hráče?

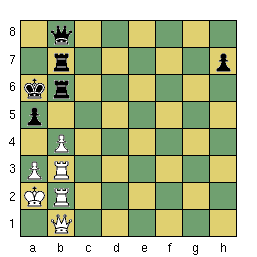
Na diagramu je pozice, která by snadno mohla vzniknout v partii, jež přešla do koncovky těžkých figur. Na tahu je bílý. První, co každého šachistu napadne je vzetí pěšcem b4 soupeřova pěšce na a5. Hned druhé co ho napadne je, že černý potom může vyměnit obě věže a dámu na b3 a vznikne koncovka králů a pěšců. A konečně třetí myšlenka bílého bude patřit vzdálenému černému pěšci h7, který může nezadržitelně kráčet do dámy, neboť jej bílý král již nedohoní. Bílý proto brát pěšce a5 nesmí. Tohle všechno napadne obyčejného klubového hráče během několika vteřin, i když se zřejmě bude ještě chvíli ujišťovat, že se v propočtu nespletl a že ten pěšec h7 opravdu uteče. A jak je na tom minimax? Počítejme spolu: 1. bxa5 Vxb3 2. Vxb3 Vxb3 3. Dxb3 Dxb3 4. Kxb3. Tady již dobrá ohodnocovací funkce uvidí průšvih - nechytatelného pěšce h7. Pokud nekontroluje uteklé pěšce musíme počítat dál: 4. ...h5 5. Kc2 h4 6. Kd2 h3 7. Ke2 h2 8. Kf2 h1D a nově postavenou dámu vidí už i jednoduchá ohodnocovací funkce. Při větvícím faktoru 38 povede algoritmus minimax na 38⁷ nebo 38¹⁶ ohodnocovacích funkcí. Propočet pozice, kde běžný klubový hráč vidí řešení za pár vteřin, bude trvat více než jeden den a noc a to v tom lepším případě. Konce výpočtu ve variantě se slabší ohodnocovací funkcí se nejspíš nedočká ani naše galaxie.

Jak můžeme časovou složitost zlepšit? Pokud chceme minimalizovat výraz x^y, můžeme zmenšovat y. To je v našem případě hloubka propočtu a ta má zásadní vliv na úroveň hry. Druhou možností je zmenšit x, větvící faktor. Jinými slovy prořezat v propočtu strom hry a některé varianty vůbec nepočítat. Existují dva typy prořezání. První typ je blízký lidskému uvažování. Člověk obvykle vybere na základě pozičního citu jeden nebo několik málo nejnadějnějších tahů a zabývá se pouze jimi. Dobří šachisté vidí nejlepší tahy v pozici velmi rychle a mýlí se jen málokdy. Častější chybou je, že šachista uvažované tahy nesprávně ohodnotí a z těch několika kandidátů nevybere nejlepšího. Ve světě počítačů tato metoda zatím nenaplnila původní očekávání. Běžně se sice zahazují zvlášť ošklivé tahy, prohlubují se nadějné varianty (což je v podstatě také ořezání - těch ostatních variant), dopočítávají se šachy a výměny figur a podobně, ale o nějakém ořezání základního propočtu stromu hry třeba na 1 až 3 tahy z typické pozice nemůže být ani řeč. Docházelo by k příliš velkým přehmatům. Počítačům prostě chybí poziční cit lidských velmistrů.

Naštěstí existuje ještě druhý typ prořezání. Nepočítat variantu, jejíž výsledek (ať už bude jakýkoli) neovlivní výběr tahu z úvodní pozice. Tohle zní na první pohled téměř neuvěřitelně. Je opravdu možné zahazovat některé varianty a přesto dojít na 100% ke správnému výsledku? Ano, je. Ukážeme si to na příkladu.

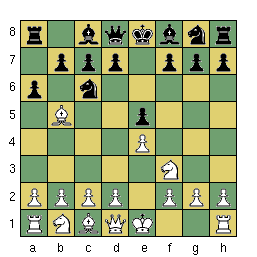
V pozici na diagramu je na tahu bílý, jedná se o známou pozici ze zahájení jménem španělská hra (1. e4 e5 2. Jf3 Jc6 3. Sb5), kde se černý brání obvyklým tahem 3. ...a6. Napadl tedy bílému střelce a ten musí hrozbu nějak pokrýt. Běžné tahy jsou nyní 4. Sa4 a Sxc6, hrát by se dalo i Sc4 a snad ještě hodně defétistické Se2, všechny ostatní tahy jsou již vyloženě špatné. Z této pozice dáme programu za úkol provést propočet do hloubky 2 půltahy. Vygeneruje tahy a zkouší jeden po druhém zahrát. Generátor tahů je lehce modifikovaný, tak aby vracel braní před ostatními tahy. Program tedy nejprve propočítá 4. Sxc6, projde všechny odpovědi černého a zjistí, že po nejlepším 4. ...dxc6 je pozice přibližně vyrovnaná. Bílý sice ztratil výhodu dvojice střelců, ale zase černému znehodnotil pěšcovou strukturu. Ohodnocení prvního tahu zatím proběhlo tak, jako v algoritmu minimax. Rozdíl nastane až u druhého tahu bílého 4. Sxa6. Jedná se o zjevnou chybu, kterou bílý odevzdává střelce za pouhého pěšce, ale minimax by musel projít všechny odpovědi, aby si to uvědomil. Tedy poctivě počítat a ohodnocovat nejen 4. ...bxa6 a Vxa6, ale i zcela nesmyslné tahy jako 4. ...Jh6 nebo g5. Modifikovanému algoritmu stačí jediná: 4. ...Vxa6 nebo bxa6. Navíc generátor tahů, který preferuje braní, vrátí jeden z uvedených tahů hned jako první. Jak program pozná, že může propočet odpovědí na 4. Sxa6 přerušit a prohlásit tah za neperspektivní? Z propočtu 4. Sxc6 si zapamatoval hodnotu nejlepší odpovědi 4. ...dxc6, tedy zhruba 0 tj. vyrovnanou pozici. Při propočtu dalších tahů (4. Sxa6) uvedenou hodnotu použijeme jako práh. Pokud jej jakákoli odpověď (4. ...bxa6 nebo Vxa6) přesáhne, propočet tahu (4. Sxa6) ukončíme, neboť již víme, že je špatný. Jinými slovy: pokud víme, že tah je špatný (= horší než nějaký jiný - zde 4. Sxc6), nemá smysl dále zkoumat, jestli není náhodou ještě o něco horší, než jsme zatím zjistili.

V příkladu jsme počítali do hloubky 2, zde se prořezávali pouze tahy černého. Při hloubce 3 a více dojde na oba hráče a jsou zde proto prahy na obě strany. Dolní mezi se říká alfa a horní beta, odtud název algoritmu: alfabeta metoda. Pokud během propočtu narazíme na variantu, která je horší než alfa, víme, že to není hlavní varianta s nejlepšími tahy za oba hráče, protože máme lepší tah. Vyjde-li varianta lépe než beta, může se ji zase vyhnout soupeř a zahrát tah, který je lepší pro něj.

Vlastní implementace není příliš složitá, je pouze třeba dát pozor na některé nepříjemné drobnosti, hlavně předávání hodnot do volaných funkcí. Posunutím o jeden půltah si alfa a beta prohodí role, neboť se změní hráč na tahu. Ze stejného důvodu je třeba hodnoty vynásobit mínus jedničkou. Stejně jako v případě algoritmu minimax musíme korektně upravovat hodnoty propočtu s matem na dohled, tak aby se např. z "Dávám mat 3 půltahem." stalo po zahrání 1. půltahu (a tím i výměnou hráče, který je na tahu) "Dostávám mat 2. půltahem".

/* Úprava cen pozic s matem na dohled. */
int blizKMatu(int cena) {
  if (cena > MNOHO) return cena + 1;
  if (cena < -MNOHO) return cena - 1;
  return cena;
}

int dalOdMatu(int cena) {
  if (cena > MNOHO) return cena - 1;
  if (cena < -MNOHO) return cena + 1;
  return cena;
}

/* Rekurzivní volání. */
int alfabeta(Pozice p, int hloubka, int alfa, int beta) {
  Tahy t;
  int i, indexNejlepsiho;
  int cena;

  /* V případě koncové pozice nebo nulové hloubky propočet ukončíme. */

  if (jsemVMatu(p)) return -MAT;
  if (remiza(p)) return 0;
  /* Dávat mat nemůžu, protože pozice je po tahu soupeře. */

  if (hloubka <= 0) return hodnotaPozice(p);

  t = generujTahy(p);

  for (i = 0; i < tahy.pocet; i++) {
    zahrajTah(p, t[i]);
    cena = -alfabeta(p, hloubka - 1, blizKMatu(-beta), blizKMatu(-alfa));
    cena = dalOdMatu(cena);
    zahrajTahZpet(p, t[i]);
    if (cena > alfa) {
      alfa = cena;
      if (cena >= beta) {
        /* Zde je právě to ořezání. */
        return beta;
      }
    }
  }

  return alfa;
}

Stejně jako u minimaxu, i zde se vyplatí propočet z kořene ošetřit zvlášť. V kořeni hrajeme vždy za jednoho hráče, proto zde není žádná beta, pouze alfa.

Tah nejlepsiTah(Pozice p, int hloubka) {
  Tahy t;
  int i, indexNejlepsiho;
  int cena, alfa;

  t = generujTahy(p);
  alfa = -NEKONECNO;

  for (i = 0; i < tahy.pocet; i++) {
    zahrajTah(p, t[i]);
    cena = -alfabeta(p, hloubka, -NEKONECNO, blizKMatu(-alfa));
    cena = dalOdMatu(cena);
    zahrajTahZpet(p, t[i]);
    if (cena > alfa) {
      alfa = cena;
      indexNejlepsiho = i;
    }
  }
  return t[indexNejlepsiho];
}

Pokračování příště

V příštím dílu se zamyslíme nad efektivitou alfabeta metody. Ukážeme si také, jak ošetřit propočet výměnných operací na konci propočtu.

Verze pro tisk