Vytváření složitých datových struktur
Odkaz na odkaz
Jednou z hodnot, které může vracet funkce ref, je "REF". To znamená, že odkaz může ukazovat na jiný odkaz. Ukažme si to opět na reprezentaci v paměti. Máme nějaký obyčejný odkaz
$x = "HODNOTA";
$r_x = \$x;
s takovou reprezentací v paměti:
| Adresa | Hodnota | Proměnná |
| 3 | ||
| 4 | ||
| 5 | "HODNOTA" | $x |
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | SCALAR(5) | $r_x |
| 11 |
Teď vytvoříme odkaz na proměnnou $r_x, která je také odkazem.
$rr_x = \$r_x;
$rr_x se v paměti uloží na novou adresu.
| Adresa | Hodnota | Proměnná |
| 3 | ||
| 4 | ||
| 5 | "HODNOTA" | $x |
| 6 | ||
| 7 | REF(10) | $rr_x |
| 8 | ||
| 9 | ||
| 10 | SCALAR(5) | $r_x |
| 11 |
$rr_x ukazuje na hodnotu proměnné $r_x, ale ta ukazuje dále na hodnotu "HODNOTA". Všechny tyto 3 proměnné ukazují postupnou dereferencí na stejnou adresu v paměti. A tak můžeme pokračovat stále dál.
Dereferenci pak provádíme postupným přidáváním dolarů. Všechny následující příkazy tisknou hodnotu na adrese 5.
print $x;
print $$r_x;
print $$$rr_x;
Při vytváření vnořených odkazů na konstantní skalár je přípustné dokonce i použití více zpětných lomítek najednou. Sice se to neužívá, ale pro zajímavost můžeme uvést alespoň ukázku.
$rrrr_x = \\\\"HODNOTA";
print $$$$$rrrr_x;
Pole odkazů na pole
Jak už víme, pole v Perlu může obsahovat pouze skalární hodnoty. Právě proto zní nadpis Pole odkazů a nikoliv Dvojrozměrné pole. Vícerozměrná pole Perl nepodporuje, ale lze je nasimulovat právě pomocí odkazů. A to až do té míry, že se dá s polem odkazů na pole pracovat prakticky stejně, "jako by se pracovalo s dvojrozměrným polem".
Vytvoření datové struktury
Pole odkazů na pole je vůbec nejjednodušší složitější datová struktura. Nejprve vytvoříme několik obyčejných polí.
@pole1 = (1, 2, 3);
@pole2 = (4, 5, 6);
@pole3 = (7, 8, 9, 10);
Odkazy na tyto pole uložíme do jiného pole. Dosáhneme toho jedním ze dvou různých zápisů. Ten první asi nikoho nepřekvapí.
@pole_odkazu = (\@pole1, \@pole2, \@pole3);
Ovšem lze toho docílit i umístěním zpětného lomítka před otevírací závorku seznamu.
@pole_odkazu = \(@pole1, @pole2, @pole3);
@pole_odkazu je právě ono pole odkazů na jiná pole. Za chvíli si ukážeme, jak se s ním pracuje.
Lepší způsob definice složitých datových struktur však nabízejí, jak víme z předchozího dílu, anonymní data. Díky nim totiž umíme vytvořit odkaz na pole bez toho, abychom toto pole měli. Použití je jednoduché - žádné proměnné @pole1, @pole2 atd. nevytváříme, ale jako prvky pole @pole_odkazu přímo předáme anonymní data.
@pole_odkazu = (
[1, 2, 3],
[4, 5, 6],
[7, 8, 9, 10]
);
Toto pole je identické s posledně vytvořeným, ale zápis je názornější.
Práce s polem odkazů na pole
Nyní, když máme vytvořenou datovou strukturu, z ní můžeme získávat hodnoty. Pole, na něž ukazuje prvek pole @pole_odkazu s indexem 0, získáme a vytiskneme tímto způsobem.
print @{$pole_odkazu[0]};
Složené závorky jsou tu proto, abychom změnili prioritu vyhodnocování. Potřebujeme získat pro index vyšší prioritu než pro dereferenci. Samotné $pole_odkazu[0] obsahuje odkaz na pole (proto se musí vyhodnotit jako první). Odkaz pak dereferencujeme.
Přístup k jednotlivým prvkům získáme přidáním indexu na konec (a samozřejmě změnou zavináče za dolar).
print ${$pole_odkazu[0]}[2];
Tento ne příliš přehledný zápis používat nemusíme. Existuje totiž operátor šipky.
print $pole_odkazu[0]->[2];
Zápis má stejný význam jako ten předchozí. Ale to není vše. Můžeme jít ještě dál a šipky mezi indexy vynechat.
print $pole_odkazu[0][2];
Zde vidíme, že práce s dvojrozměrným polem z jiných jazyků a polem odkazů na pole se prakticky neliší. Proto budeme dále tyto dva pojmy pro lepší pochopitelnost textu zaměňovat.
Počítání s maticemi
Abychom si procvičili práci s datovými strukturami, ukážeme si dále několik příkladů. Typickou ukázkou pro použití pole polí jsou operace s maticemi. Matice není nic jiného, než obdélníkové dvojrozměrné pole. Rozebereme si součet a součin matic. V archivu CPAN existují moduly, které tyto operace zvládnou samy (například Math::MatrixReal), my si však napíšeme programy vlastní.
Součet matic
Implementujeme si funkci, která sečte 2 matice. Sčítané matice musejí mít stejný počet řádků a sloupců. Pro součet matic A a B platí:
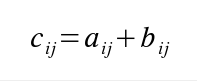
Součet matic
pro všechny dvojice ij, kde C je výsledná matice a aij, bij, resp. cij jsou odpovídající prvky matice A, B, resp. C na řádku i a sloupci j.
Sčítat matice bude procedura secti_matice. secti_matice přijme jako argument odkazy na 2 matice. V této proceduře musí být také zkontrolováno, zda je vůbec možné matice sečíst. To znamená zkontrolovat, zda mají obě matice stejný počet řádků a sloupců. Budeme předpokládat, že matice jsou obdélníkové.
Než se pustíme do řešení, poznamenejme, že v praxi bychom operace s maticemi nejspíše prováděli pomocí objektů. Jelikož čas objektů v seriálu teprve nastane, spokojíme se s neobjektovým provedením.
Pojďme tedy začít pracovat na funkci secti_matice. Z přijatých odkazů je snadné získat počet řádků. Stačí dereferencovat a skalární vyjádření získaných polí porovnat.
sub secti_matice {
my($r_A, $r_B) = @_;
die "Matice A a B maji jiny pocet radku!\n" if @$r_A != @$r_B;
...
}
Pro názorost nyní v podprogramech voláme die, ale ve výsledném programu tato volání nahradíme.
Dále musíme zkontrolovat, zda mají matice i stejný počet sloupců. Uděláme to pro nulté řádky matic. (nultý prvek obsahuje odkaz na pole - toto pole musí mít u obou matic stejný počet prvků).
die "Matice A a B nemaji stejny pocet sloupcu!\n" if scalar @{$r_A->[0]} != scalar @{$r_B->[0]};
Předpokládáme, že všechny řádky mají stejný počet sloupců.
Nyní jsou všechny podmínky splněny, takže můžeme matice sečíst. Máme počet řádků i počet sloupců. Zbývá jen napsat cyklus, ve kterém vytvoříme matici C.
my $radku = @$r_A;
my $sloupcu = @{$r_A->[0]};
for (my $i=0; $i<$radku; $i++){
for(my $j; $j<$sloupcu; $j++){
$C[$i][$j] = $A[$i][$j] + $B[$i][$j];
}
}
To je podprogram secti_matice. Nyní napíšeme ukázkové tělo programu, který ho používá.
my @A = (
[2, 3, 5, 2],
[7, -8, 12, 4],
[4, 5, 0, 7]
);
my @B = (
[8, 7, 5, 8],
[16, -4, -10, 0],
[0, -1, 7, 0]
);
my @C = secti_matice(\@A, \@B);
tiskni_matici(\@C);
Podprogram tiskni_matici bude vypadat podobně jako secti_matice. Lišit se bude jen v tom, že odpadnou kontroly a místo sčítání se bude tisknout.
sub tiskni_matici {
my ($r_matice) = @_;
my $radku = @$r_matice;
my $sloupcu = @{$r_matice->[0]};
for (my $i=0; $i<$radku; $i++){
for (my $j; $j<$sloupcu; $j++){
printf "%8.1f ", $$r_matice[$i][$j];
}
print "\n";
}
}
Součin matic
Vytvoříme další podprogram pro počítání s maticemi. Tentokrát to bude o jeden cyklus složitější, protože půjde o násobení. Součin matic má význam jen tehdy, má-li matice A stejný počet sloupců jako matice B řádků. Připomeňme si opět vztah.
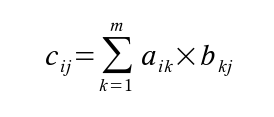
Součin matic
pro všechny dvojice ij, kde C je výsledná matice, aij, bij, resp. cij jsou prvky matice A, B, resp. C na řádku i a sloupci j a m je počet sloupců matice A a zároveň počet řádků matice B.
Stejně jako u součtu matic musíme zkontrolovat zda má násobení smysl. Počet sloupců matice A musí být stejný jako počet řádků matice B.
die "Matice A ma jiny pocet sloupcu nez matice B radku!\n" if @{$r_A->[0]} != @$r_B;
Pokračujme ale dále v podprogramu vynasob_matice. Teď totiž přichází na řadu hlavní část programu.
Vnořeny do sebe budou 3 cykly. Každý řádek matice A (1. cyklus) bude vynásoben se všemi sloupci matice B (2. cyklus). Každé násobení řádek × sloupec bude navíc rozloženo na násobení odpovídajících si prvků (pro každý prvek se bude počítat aik * bkj). Proto musíme použít 3. cyklus o tolika iteracích, kolik má A sloupců, resp. B řádků.
for (my $i=0; $i<$A_radku; $i++){
for (my $j; $j<$B_sloupcu; $j++){
$prvek = 0;
for (my $k=0; $k<$A_sloupcu; $k++){
$prvek += $r_A->[$i][$k] * $r_B->[$k][$j];
}
$C[$i][$j] = $prvek;
}
}
Teď jen upravit tělo programu a vstupní matice a můžeme spustit program. Podprogram tiskni_matici upravovat nemusíme.
Hash polí
Než se pustíme do libovolně složitých datových struktur, musíme si ukázat, jak do jejich tvorby zapojit hashe. Proto se tedy ještě krátce podíváme na další datovou strukturu, kteroužto je hash polí. Takový hash obsahuje jako své hodnoty odkazy na pole.
Hash bude obsahovat jednoduchou databázi knih, tříděných podle témat. Tedy každému tématu přiřadíme několik knih. Anonymní pole s názvy knih budou hodnotami hashe.
%knihy = (
"Perl" => ["Programování v Perlu pro pokročilé", "Perl pro zelenáče",
"Myslíme v jazyku Perl"],
"C++" => ["Mistrovství v C++", "Myslíme v C++"],
"Java" => ["Java - příručka programátora", "Začínáme programovat"],
);
A teď můžeme se strukturou pracovat. Pokud chceme vypsat knihy o Perlu, zapíšeme následující příkaz.
print "Knihy o Perlu: ", @{$knihy{"Perl"}};
Podobně, chceme-li přidat nějakou další knihu.
push(@{$knihy{"Java"}}, "Jáva - dějiny ostrova");
Na závěr poznamenejme, že při vytváření anonymních polí je leckdy výhodné použití ozávorkování pomocí qw. V našem případě seznamu knih to bohužel použít nelze, ale pokud by položky byly jednoslovné, mohli bychom psát zhruba toto.
%struktura = (
"Téma1" => [qw(polozka1 polozka2 polozka3 polozka4)],
"Téma2" => [qw(polozka1 polozka2 polozka3 polozka4)],
"Téma3" => [qw(polozka1 polozka2 polozka3 polozka4)],
);