Úvod do teorie - základní pojmy
Hned v úvodu začneme tím, co je to vlastně graf. Jednoduše řečeno, není to nic jiného, než množina vrcholů a hran,
přičemž jednotlivé vrcholy jsou navzájem hranami spojeny a to tak, že každá hrana spojuje právě dva vrcholy. Je však
nutné popsat graf trochu lépe, proto tedy správná definice grafu zní:
Obyčejný, nebo též jednoduchý, neorientovaný graf je uspořádáná dvojice G = (V, E), kde V je množina vrcholů a
E je množina hran - množina vybraných dvouprvkových podmnožin množiny vrcholů.
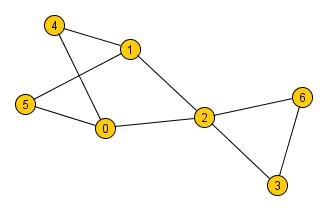
Na obrázku je uvedena ukázka grafu, který má 7 vrcholů a 9 hran. Je vidět, že každá hrana spojuje právě dva různé
vrcholy. Takovým vrcholům se pak říká sousední. Jako příklad sousedních vrcholů lze uvést třeba vrcholy 2 a 6,
0 a 5 apod. Vrcholy 0 a 1 ale mezi sebou hranu nemají, tudíž nejsou sousední. To však ještě nutně nemusí znamenat, že
se z jednoho vrcholu do druhého nejde dostat. Z vrcholu 0 je možné jít do vrcholu 4 a z toho pak do vrcholu 1. Tím
jsme vlastně našli jednu cestu, což je další pojem, který se v souvislosti s grafy používá.
Cesta délky n má (n + 1) vrcholů, spojených za sebou n hranami.
Cesta, kterou jsme si uvedli my, má tedy délku 2. Určitě ale není těžké najít jinou cestu délky 2. Je snad tedy
jasné, že cest z jednoho vrcholu do druhého může v grafu existovat více, ne jen jedna. Je to stejné jako například s
městy. Z Prahy do Ostravy můžete jet přímo po dálnici, což bude asi nejkratší cesta (nejkratší ve smyslu vzdálenosti),
ale také můžete jet přes České Budějovice a cesta bude delší. Příklad, který jsem uvedl, lze snadno převést na graf,
kde města budou vrcholy a hrany budou jednotlivé cesty. Zatím jsme ale pracovali s grafy, kde jednotlivé hrany byly
stejné dlouhé. V reálném světě tomu tak samozřejmě není, vzdálenost mezi Prahou a Českými Budějovicemi je určitě jiná,
než vzdálenost mezi Prahou a Ostravou. Aby se i tato skutečnost dala reprezentovat pomocí grafů, zavedl se pojem tzv.
váženého grafu.
Vážený graf je graf, společně s ohodnocením svých hran reálnými čísly.
Tato definice neznamená nic jiného, než to, že se jedná o obyčejný graf, který má ale navíc u svých hran čísla, která udavájí
váhu (velikost). Z toho vyplývá, že hrany v grafu mají různou velikost. Tyto grafy nám pak dávají větší možnost, jak vyjádřit
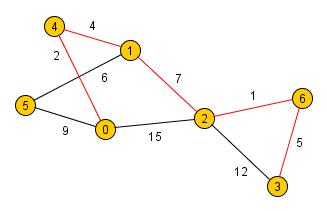
něco skutečného, například již zmíněné spojení mezi městy. Na následujícím obrázku je ukázka váženého (ohodnoceného) grafu, na
kterém je vyznačena nejkratší možná cesta (červenou barvou) z vrcholu 0 do vrcholu 3 - schválně si všimněte, že cesta vede přes 5 hran, přičemž je
možné, najít cestu pouze přes 2 hrany, nicméně tato cesta bude delší. To je dáno tím, že v tuto chvíli nás nezajímá počet hran,
ale jejich ohodnocení.
V tomto malém grafu asi není problém během okamžiku najít nejkratší cestu z jednoho vrcholu do druhého. V mnohem větších grafech
už to tak snadné není, proto k nalezení nejkratší cesty v grafu je algoritmus, konkrétně Dijkstrův algoritmus. K němu se dostaneme
za chvíli, nejprve si ukážeme jednodušší algoritmus pro výpočet metriky grafu.
Metrika grafu
Dříve, než přejdeme k samotnému algoritmu, který je mimochodem poměrně jednoduchý, řekneme si, co to vlastně metrika grafu je.
Není to nic jiného, než soubor vzdáleností mezi všemi dvojicemi vrcholů grafu. Je to tedy vlastně matice (dvourozměrné pole),
kde prvek d[i][j] udává vzdálenost mezi vrcholy i a j. Pro názornost si uvedeme ukázku metriky grafu z předchozího
obrázku.
| [i][j] | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 6 | 13 | 19 | 2 | 9 | 14 |
| 1 | 6 | 0 | 7 | 13 | 4 | 6 | 8 |
| 2 | 13 | 7 | 0 | 6 | 11 | 13 | 1 |
| 3 | 19 | 13 | 6 | 0 | 17 | 19 | 5 |
| 4 | 2 | 4 | 11 | 17 | 0 | 10 | 12 |
| 5 | 9 | 6 | 13 | 19 | 10 | 0 | 14 |
| 6 | 14 | 8 | 1 | 5 | 12 | 14 | 0 |
Abychom mohli napsat algoritmus, který nám dokáže metriku vypočítat, musíme nejprve do programu jako vstup zadat náš graf. Otázka je tedy jasná - jakým způsobem reprezentovat graf v paměti? Možnost není jen jedna, v tomto případě však bude nejvhodnější použít tzv. matici sousednosti. Jedná se o dvourozměrné pole (např. G), ve kterém G[i][j] = x znamená, že mezi vrcholy i a j je hrana délky x. Tam, kde hrana není, bude hodnota 0. V jazyce C++ bychom matici sousednosti zapsali takto:
const int N = 7; // pocet vrcholu
int G[N][N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
G[i][j] = 0;
G[0][2] = G[2][0] = 15;
G[0][4] = G[4][0] = 2;
G[0][5] = G[5][0] = 9;
G[1][2] = G[2][1] = 7;
G[1][4] = G[4][1] = 4;
G[1][5] = G[5][1] = 6;
G[2][3] = G[3][2] = 12;
G[2][6] = G[6][2] = 1;
G[3][6] = G[6][3] = 5;
Budeme počítat metriku, čili matici, proto potřebujeme pole, které si označíme například d. Na začátku bude hodnota prvku d[i][j] udávat délku hrany mezi vrcholy i a j, nebo "nekonečno" v případě, že hrana mezi těmito vrcholy není (nekonečno budeme reprezentovat konstantou INT_MAX / 2). Poté při každém dalším kroku algoritmu se vzdálenost mezi vrcholy buď zmenší, nebo zůstane stejná (nikdy se nezvětší). My vlastně v každém kroku přidáme jeden konkrétní vrchol a zjistíme, zda je možné se díky tomuto vrcholu dostat z i do j kratší cestou.
// vypocet metriky
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
if (i == j)
d[i][j] = 0;
else if (G[i][j] != 0)
d[i][j] = G[i][j];
else
d[i][j] = INT_MAX / 2;
for (int k = 0; k < N; k++)
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
Trochu složitější je to v následujících třech cyklech. Iterační proměnná k nám vlastně symbolizuje nějaký vrchol, i a j jsou vrcholy, mezi kterými hledáme nejkratší cestu. My poté buď ponecháme vzdálenost mezi vrcholy takovou, jaká je momentálně v matici metriky, nebo na pozici d[i][j] uložíme cestu kratší, která vede právě přes vrchol k. Pro dokonalé pochopení doporučuji si algoritmus trochu projít, není nikterak složitý. Až algoritmus skončí, máme v poli d uloženou metriku grafu, čili soubor vzdáleností mezi všemi vrcholy.
Podíváme-li se na algoritmus z trochu jiného pohledu, musíme konstatovat, že implementačně není příliš složitý a zjistí nám nejkratší cesty mezi všemi vrcholy. Má však jednu (a poměrně velkou) nevýhodu - obvykle potřebujeme znát nejkratší cestu pouze mezi dvěma konrétními vrcholy, ale tento algoritmus nám vypočítá nejkratší cesty mezi všemi vrcholy, což je dosti zbytečné. Proto se tento algoritmus používá opravdu jen v konkrétních případech, kdy nás zajímají všechny vzdálenosti. V případě, že nás zajímají pouze nejkratší cesty z jednoho konkrétního vrcholu, je mnohem lepší použít Dijkstrův algoritmus.
Dijkstrův algoritmus
Tento algoritmus je sice o něco složitejší než výše uvedený, je však rychlejší. Na základě tohoto algoritmu je možné napsat program, který bude vyhledávat vlakové či autobusové spojení. Nyní se podívejme na popis, jak algoritmus funguje.
Všechny vrcholy jsou uchovávány v prioritní frontě, přičemž jsou řazené dle vzdálenosti od zdroje (zdrojem rozumíme vrchol, ze kterého hledáme cesty). V prvním průchodu má pouze zdroj vzdálenost 0, ostatní uzly mají zatím vzdálenost nekonečno (INT_MAX). Poté algoritmus vybere z fronty vrchol, který má nejvyšší prioritu, čili vrchol, který má nejmenší vzdálenost od zdroje. Tento vrchol zařadí mezi zpracované vrcholy. Následně projde všechny nezpracované sousední vrcholy tohoto zpracovaného vrcholu, přidá je do fronty a ověří, zda jsou blíže ke zdroji, než byly předtím. V případě, že zjistí, že některý sousední vrchol je nyní blíže, nastaví tomuto vrcholu novou, menší vzdálenost. Po průchodu všech sousedů se algoritmus vrací zpět na začátek. Algoritmus skončí, jakmile jsou jako zpracované označené všechny vrcholy. Poté máme k dispozici délky nejkratších cest z vrcholu, který jsme si vybrali jako zdroj.
Ukázku, jak napsat Dijkstrův algoritmus v jazyce C++, si můžete stáhnout zde. Graf je opět reprezentován pomocí matice sousednosti. Výstupem z programu jsou nejkratší vzdálenosti z vrcholu 0 do všech ostatních vrcholů (v kódu je graf, u kterého jsme výše počítali metriku). To, že algoritmus funguje správně, si tak můžete ověřit tím, že se podíváte na výstup programu a zjistíte, že je totožný s prvním (lepší je možná nultým, neboť hledáme cesty z vrcholu 0) řádkem (nebo sloupcem) matice metriky.