Trocha teorie
Reálná funkce dvou reálných proměnných je zobrazení, které přiřazuje uspořádané dvojici reálných čísel (definiční obor) jednoznačně reálné číslo. Grafem takovéto funkce je pak množina bodů v třírozměrném eukleidovském prostoru. Jako příklad funkce dvou proměnných můžeme vzít model zemského povrchu: každému bodu o dané zeměpisné šířce a délce je přiřazena nadmořská výška. Tolik asi na úvod.
Praxe
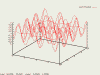
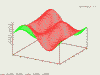
Základním příkazem v Gnuplotu pro práci s grafy funkcí dvou proměnných je splot, jehož nejdůležitějším argumentem je požadovaná funkce (jako proměnné se používá x, y):
Jak vidíte na obrázku, výsledek není příliš vhodný k publikaci. Jako první zkusíme změnit rozmezí os. U "obyčejných" funkcí v jedné proměnné k tomu účelu sloužil příkaz set s parametry xrange a yrange. Asi Vás příliš nepřekvapí, že se tento příkaz použije i v tomto případě, pouze přibude parametr zrange pro úpravu osy z. Tímto způsobem nastavíme měřítko pro všechny grafy v rámci jedné relace, pro změnu jediného grafu použijeme následující zápis:
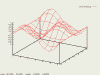
splot [x1:x2][y1:y2][z1:z2] f(x,y) # nastav meze na všech osách splot [x1:x2] f(x,y) # nastav meze pouze na ose x splot [][y1:y2] f(x,y) # nastav pouze osu y splot [][][z1:z2] f(x,y) # nastav pouze osu z set xrange [0:2*pi] # nastav globálně meze na ose x set yrange [0:2*pi] # nastav globálně meze na ose y set autoscale z # automatické nastavení mezí na ose hodnot (z) replot # překresli graf
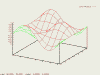
Nyní už náš graf vypadá trochu lépe, ale stále není ideální. Zkusíme nevykreslovat zakryté části grafu - příkazem set hidden3d. Pro opětovné vykreslení i neviditelných míst zavolejte unset hidden3d.
set hidden3d # zobraz pouze viditelné replot # překresli graf
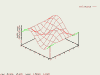
Někdy se může hodit podívat se na graf z jiného úhlu a jiné vzdálenosti. I zde přijde ke slovu příkaz set, nyní s parametrem view h, v, z. Hodnota h představuje horizontální úhel (mezi pozorovatelem a horizontálou), v znamená vertikální úhel (mezi pozorovatelem a vertikálou), konečně z představuje míru přiblížení nebo oddálení (zoom). Výchozí hodnoty jsou 60 pro h, 30 pro v a 1 pro z. Pro přiblížení grafu používejte hodnoty z větší než 1, naopak pro oddálení menší než 1.
set view 45, 45, 0.75 # změna pozice pozorovatele replot set view ,,2 # přiblížení pozorovatele ke grafu replot set view 60,30,1 # návrat na výchozí pohled
Druhým způsobem je nakreslený graf popadnout myší a s pomocí metody drag&drop (popřípadě kurzorových kláves) jej natočit podle potřeby.
Pro zvýšení přesnosti grafu tu máme příkaz set isosamples sx, sy, kde sx (sy) představují počet vzorků na ose x (y), vyšší hodnoty vylepšují vzhled grafu, ale také procesorový čas potřebný k vykreslení (100*100 vzorků se na mém AMD XP 2600+ počítá asi 30 sekund).
Poslední možnost, kterou k tématu funkcí dvou proměnných zmíním, jsou ekvipotenciální čáry. Ekvipotenciální čára je množina bodů prostoru, které mají stejnou hodnotu veličiny, v případě modelu zemského povrchu se jedná o vrstevnice. Gnuplot zvládá 4 režimy vykreslování těchto čar - nevykreslovat, vykreslovat přímo do grafu funkce, vykreslovat projekci do roviny x, y a konečně vykreslit projekci a současně na graf funkce:
# kresli ekvipotenciální křivky na plochu grafu set contour surface # kresli projekci ekvipotenciálních křivek do roviny x,y set contour base # kombinace předchozích způsobů set contour both # vypni vykreslování ekvipotenciálních čar unset contour
Nastavování popisků grafu, os a mřížky se provádí úplně stejně jako v případě funkce jedné proměnné.
Polární souřadnice
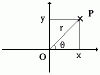
Bod v rovině lze určit několika způsoby - asi nejpřirozenějším jsou kartézské souřadnice. Jejím základem jsou dvě kolmé přímky (osy x a y), které se protínají v počátku O. Polohu bodu pak jednoznačně určíme jako průsečík přímky rovnoběžné s osou x a přímky rovnoběžné s osou y. Ne vždy je ovšem použití kartézského systému nejvhodnější, například při studiu kruhových pohybů (rovnice popisující kyvadlo) se používají polární souřadnice. Pokud povedeme bodem P kružnici se středem v počátku O a označíme-li úhel mezi polopřímkou OP a poloosou x theta (θ), pak polární souřadnice bodu P budou R=|OX|, theta. Kartézské souřadnice lze z polárních jednoduše dopočítat:
Rovnici křivky v polárních souřadnicích můžeme vyjádřit jako:
Pro zapnutí polárních souřadnic se zavolá příkaz set s parametrem polar. Při kreslení v polárních souřadnicích se používá proměnná t, která má význam polárního úhlu (theta). Při výchozím nastavení se mez t bere interval od 0 do 2*pi. Změna se provede příkazem set trange [theta1: theta2]. Pro změnu jednotek z radiánů na stupně použijte set angles degrees (radians pro radiány).
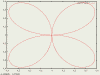
set polar # aktivuj polární souřadnice plot cos(t)*sin(t) # čtyřlístek :-) set trange [0:pi/2] # nastavení rozsahu t replot # překreslení grafu unset polar # návrat do kartézského systému
Pro zisk podrobnější nápovědy napište help polar
Parametrické křivky
Na závěr stručně zmíním postup vykreslování parametricky zadaných křivek. Zápis y=f(x) explicitně vyjadřuje závislost veličiny y na veličině x. Závislost x na y lze zadat i zprostředkovaně, pomocí parametru:
Pro vykreslení parametrické křivky je potřeba nejprve aktivovat režim parametrického zadávání a poté za příkaz plot přidat rovnice pro x a y v proměnné t:
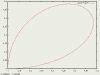
# zapni režim parametrického zadávání set parametric plot sin(t), cos(t) # parametrická křivka
Výsledkem by měla být jednotková kružnice, ovšem kvůli rozdílnému měřítku na osách x, y nejspíše uvidíte elipsu. Pro srovnání měřítka na osách napište:
Tento příkaz nastaví poměr měřítka osy y k měřítku na ose x na zadanou hodnotu. Gnuplot umí vykreslovat parametricky zadané plochy v prostoru, za příkaz splot je třeba přidat parametrické vyjádření pro souřadnice x, y a z v proměnných u, v:
set parametric # zapni parametrické zadání # vykresli parametrickou plochu # x(u, v) = cos(u)*cos(v) # y(u, v) = cos(u)*sin(v) # z(u, v) = sin(u) splot cos(u)*cos(v),cos(u)*sin(v),sin(u) set hidden3d # kresli jen viditelné set isosamples 50,50 # nastav rozlišení grafu replot # překresli graf unset parametric # konec parametrického zadávání
To je pro tento díl vše, příště se snad už nebude zabývat žádnou složitější matematikou, ale zpracováním datových souborů.