
|
|
 Šachové myšlení (4) - vylepšení alfabety
Šachové myšlení (4) - vylepšení alfabety
Dnes si spočítáme časovou složitost alfabeta metody, užijeme si tedy i trochu matematiky. Efektivita algoritmu silně závisí na velikosti (alfa, beta) intervalu. To poskytuje obrovský prostor pro nejrůznější heuristiky spojené s tříděním tahů podle jejich nadějnosti.
17.7.2006 09:00 | Jan Němec | czytane 14875×
RELATED ARTICLES
KOMENTARZE
Složitost alfabeta metody
Minule jsme se zamysleli nad časovou složitostí minimaxu, vyšlo nám xy, kde x je větvící faktor (v šachách asi 38) a y je hloubka propočtu. Zjistili jsme, že podobný algoritmus díru do světa rozhodně neudělá. Proto jsme navrhli jeho vylepšení jménem alfabeta metoda. Zamyslíme se nyní nad časovou složitostí alfabety, přesněji řečeno nad počtem vykonaných ohodnocovacích funkcí při propočtu do pevné hloubky ve stromu s konstantním větvícím faktorem.
V případě minimaxu to bylo jednoduché, program musel odhadovat hodnotu pozice ve všech listech stromu propočtu. Prořezání alfabeta metody výpočet časové složitosti algoritmu komplikuje, čím víc se nám podaří prořezávat, tím méně listů budeme ohodnocovat. Míra prořezání zase závisí na ohodnocení listů a na pořadí, ve kterém tahy procházíme. Algoritmus více prořezává, pokud jsou lepší varianty prohledávány jako první. Optimálně, pokud v každé pozici propočtu začneme procházet tahy od nejlepšího. Přesněji řečeno od toho tahu, který bude nakonec vyhodnocen jako nejlepší. (Pochopitelně to nemusí nutně být objektivně nejlepší tah.) Důvod je zřejmý: dobrý tah nejvíce posune práh alfa směrem nahoru, tím pádem se při propočtu následníků dalších tahů sníží hodnota beta a (pokud opět prohledávám od nejlepšího tahu) již první následník způsobí přetečení bety a odříznutí všech dalších následníků, které tak nebude třeba propočítávat. Jasnější to může být na příkladu ze španělské hry v minulém dílu.
Zkusme si teď spočítat časovou složitost alfabeta metody při optimálním pořadí prohledávaných tahů v případě propočtu do hloubky y a konstantním větvícím faktoru x.
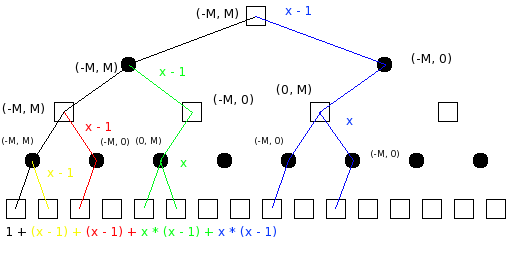
Na obrázku je binární strom, jako kdyby v každé pozici byly právě dva přípustné tahy, ale obrázek zároveň znázorňuje strom hry s vyšším větvícím faktorem x, třeba šachových zhruba 38. V tom případě levá větev představuje první (nejlepší) tah a pravá větev všechny ostatní. Ve vrcholech označených čtverečkem je na tahu bílý, kolečkem černý. Propočet provádíme do hloubky 4 půltahy, takže 16 spodních čtverečků představuje koncové pozice, ve kterých přijde na řadu ohodnocovací funkce. Abychom zajistili optimální uspořádání tahů (začátek od nejlepšího), bude ohodnocovací funkce vracet vždy 0. Pro názornost si představme, že program počítá třeba procházku dvou králů po prázdné šachovnici, tam je cena každé pozice opravdu 0 tj. remíza. To, že v podobné pozici nemá smysl provádět propočet, nás teď nemusí trápit. Nezajímá nás nejlepší tah v elementární remízové pozici, ale složitost algoritmu v optimálním případě. Interval v kulatých závorkách znamená interval (alfa, beta) při vstupu rekurzivního algoritmu do dané pozice. M je konstanta pro mat, tedy fakticky jakási naše náhrada nekonečna.
Zkusme si ručně odsimulovat chod alfabeta metody. Na počátku je okénko (alfa, beta) zcela otevřené, hledáme tah s hodnotou od mínus matu do matu. Program se nejprve zanořuje stále doleva a hlouběji ve stromu propočtu, interval zůstává stejný. Úvodní cestu algoritmu znázorňují černé hrany. Po vyhodnocení nejlevějšího listu se vrátí do jeho rodiče, tomu budeme říkat nadlist. List měl hodnotu 0, sevřeme tedy okénko na (0, M). K ořezání dojde, pokud překročíme betu. Ta je ovšem fakticky nekonečno, takže jsme si sevřením okénka příliš nepomohli a musíme projít i další (žluté) tahy. V binárním stromu na obrázku je jen jeden, ve skutečném stromu x - 1. Poté se vrátíme do rodiče nejlevějšího nadlistu s hodnotou 0 a sevřeme tedy i jeho interval na (0, M). Při propočtu jeho následníků (podstrom s červenými hranami) se interval (0, M) otočí na (M, 0). To už je pro efektivitu algoritmu významné. Je-li beta 0, můžeme ji překročit nebo alespoň vyrovnat a způsobit tak ořezání všech hran kromě prvních vedoucích ze všech vrcholů označených černým kolečkem v červeném podstromu. Na obrázku tak místo dvou ohodnocovacích funkcí budu počítat jen jednou, v obecném případě pak místo x * (x - 1) počítám x - 1 krát. V šachách tak bude průchod touto částí stromu oproti minimaxu 38 krát rychlejší. Zelenou a modrou část stromu si jistě zvládne odsimulovat každý sám.
Sečíst všechny vykonané ohodnocovací funkce již není příliš obtížné. Barevné stromy mají větvící faktory závislé na patrech, jde o posloupnost x - 1, 1, x, 1, x, 1, .... Ohodnocovacích funkcí tedy bude 1 + (x - 1) + (x - 1) + x * (x - 1) + x * (x - 1) + x2 * (x - 1) + x2 * (x - 1) + ... Pro sudou hloubku y snadno počet ohodnocovacích funkcí sečteme:
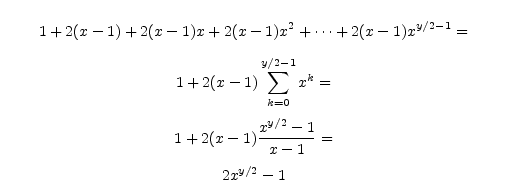
Pro liché hloubky y to vyjde jen nepatrně hůř, samozřejmě výraz můžeme shora odhadnout výsledkem pro sudé y + 1.
V úpravách výrazu jsem použil vzoreček pro součet prvních n členů geometrické posloupnosti, který si buď pamatujeme ze střední školy nebo odvodíme prostým roznásobením závorek, neboť se zde všechny členy s výjimkou nejvyššího a nejnižšího poodečítají:
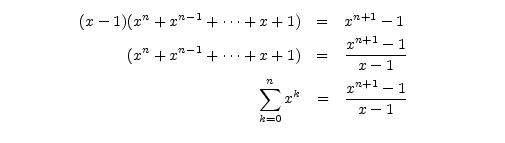
To byla časová složitost (počet ohodnocovacích funkcí) alfabeta metody v nejlepším případě. A co v případě nejhorším? Lze snadno ukázat, že při "nevhodném" ohodnocení listů a propočtu tahů od nejhoršího k nejlepšímu si oproti minimaxu neušetříme vůbec nic a budeme muset ohodnotit všech xy pozic.
Co si z této analýzy odnést? Jednak vzoreček pro optimální případ alfabeta metody oproštěný o (nezajímavé) aditivní a multiplikativní konstanty tj. výraz xy/2 a jeho srovnání s minimaxovým xy. Je vidět, že při správném pořadí propočtu tahů se ve stejném čase dostanu s alfabeta metodou dvakrát hlouběji než s minimaxem. Dalším důležitým závěrem je, že složitost alfabeta metody silně závisí na pořadí tahů. To, do jaké míry se přiblížíme dvojnásobné hloubce minimaxu, je především věcí heuristik pro třídění tahů.
Víme tedy, o co se máme snažit: počítat nejlepší tah jako první, ale na první pohled se zdá, že jsme si moc nepomohli. K tomu, abychom zrychlili výpočet bychom potřebovali znát výsledek tohoto výpočtu předem. Naštěstí není nutné začít vždy nejlepším tahem, k velkému zrychlení algoritmu stačí jen, pokud většinou bude jeden z dobrých tahů propočten jako jeden z prvních. Na to nepotřebujeme znát výsledek propočtu, stačí nám jeho rychlý (a nepřesný) odhad. Podívejme se na konkrétní heuristiky. V silných programech nebude implementována jen jedna z nich, ale půjde o nějakou jejich kombinaci. Například přiřadíme tahům nějaké ohodnocení podle jednotlivých heuristik, tato ohodnocení sečteme a tahy podle součtu setřídíme.
Sežer co můžeš
Způsobí-li tah změnu materiálu (braní nebo proměna pěšce) přiřadíme mu bonus podle hodnoty sebraného kamene. Můžeme rovněž mírně preferovat braní méně hodnotným kamenem. Většina nedostatečně informovaných šachistů by možná tuto metodu zavrhla. V pozicích, které nastávají ve velmistrovských partiích se totiž obvykle nevyplácí brát. Hráč má běžně k dispozici několik nevýhodných braní, kterými může vzít krytý kámen svým cennějším kamenem. Naopak výhodných braní jako například sebrání cenného nebo nekrytého kamene či výhodná výměna je v průměrné pozici z partie velmi málo, většinou nula. Vtip celé metody ale spočívá v tom, že běžná pozice z partie vypadá úplně jinak než běžná pozice z propočtu. Navzdory množství prořezávacích heuristik je naprostá většina počítaných variant nesmyslná a větev propočtu obsahuje velmi chybné tahy, jako například nastavení dámy nebo sebrání krytého pěšce. V těchto pozicích bývá často braní tím nejlepším tahem.
Historická heuristika
Je založená na následující myšlence: pokud byl tah dobrý v jedné variantě, nejspíš bude dobrý i v jiné. Popíšeme si tři typy této metody.
Globální tabulka tahů
Program si musí nějak pamatovat tahy. Informace odkud a kam se táhne, případně typ nové figury po proměně pěšce se při troše snahy vejde do 16 bitů. Pořídíme si tedy (jednorozměrnou) tabulku velikosti 216, pro každý možný tah jeden byte. Na počátku propočtu tabulka obsahuje samé nuly. Když se nějaký tah ukáže jako dobrý (větší než aktuální hodnota alfa). Zvětším hodnotu jeho políčka v tabulce. Když potom po vygenerování třídím tahy, uvažuji ještě také hodnotu této heuristiky. Jak přesně se mají zvětšovat hodnoty v tabulce je složitá otázka. Je zřejmé, že dobré tahy z pozic vzdálenějších od kořene mají menší význam než dobré tahy z pozic blízkých kořeni. Je to tím, že průměrná pozice z propočtu je bližší kořeni než nějakému listu ze vzdálené větve. Do tabulky se neustále přičítá, časem tedy přeteče. V tom případě do tabulky dosadím maximální hodnou 255 a všechny prvky tabulky vydělím dvěma. Například.
Nejlepší tahy pro danou hloubku
Pro každou hloubku zanoření v propočtu si pamatuji poslední dva zlepšující tahy. Tyto tahy dostanou při propočtu v tomto zanoření speciální bonus. Oproti globální tabulce má metoda tu výhodu, že se více týká aktuální pozice a příslušné hloubky, chová se tedy lokálně. Tím pádem většinou preferuje zlepšující tahy z blízkých uzlů a u nich je opravdu dost velká pravděpodobnost, že budou dobré i v počítané pozici. Nevýhodou je, že ohodnocuje jen relativně málo tahů (přesně 2).
Hlavní varianta
Program si uchovává v tabulce dosavadní hlavní variantu, tedy větev výpočtu při optimální hře (optimální ve smyslu ohodnoceni listů) obou hráčů. Tah, který přísluší k hlavní variantě bude zřejmě dobrý i v celé řadě jiných variant, a proto získává bonus. Varianty se ukládají do matice, využívá se ale jen horní trojúhelník. V jednom políčku matice je jeden tah. Jsem-li při propočtu v nějakém uzlu, počítám v tomto okamžiku vlastně hodnotu všech pozic na cestě z kořene do našeho uzlu. V i-tém řádku (od diagonály dál) si uchovávám nejlepší dosavadní variantu z i-té pozice na cestě od kořene. Dejme tomu, že v hloubce i došlo k nalezení zlepšujícího tahu. V řádku i mám původní nejlepší variantu (od naší pozice dál) a v řádku i+1 je zlepšující varianta (neboť jsem ji právě teď počítal). Za této situace musím zkopírovat i+1-ní řádek na pozici i-tého (z něj zůstane jen první tah na diagonále). Zní to možná trochu komplikovaně, ale implementace obtížná není
Pokračování příště
Uvedené heuristiky lze snadno a efektivně implementovat již v generátoru tahů. Třídit tahy nebo zvyšovat efektivitu jiným způsobem však můžeme i ve vlastním propočtu, zejména v souvislosti s takzvanou kaskádovou metodou. Podíváme se také na některé metody prohlubování propočtu.
Šachové myšlení (1) - nejjednodušší program
Šachové myšlení (2) - minimax
Šachové myšlení (3) - alfabeta
Šachové myšlení (5) - kaskádová metoda, prohlubování
Šachové myšlení (6) - Prořezávání
Šachové myšlení (7) - Haš tabulky
Šachové myšlení (8) - Haš funkce
Šachové myšlení (9) - Reprezentace pozice
Šachové myšlení (10) - Tahy
Šachové myšlení (11) - Ohodnocovací funkce
Šachové myšlení (12) - Knihovna zahájení
Šachové myšlení (13) - Databáze koncovek
Previous Show category (serial) Next
|
|
||
|
KOMENTARZE
Nie ma komentarzy dla tej pozycji. |
||
|
Tylko zarejestrowani użytkownicy mogą dopisywać komentarze.
|
||
| 1. |
Pacman linux Download: 5778x |
| 2. |
FreeBSD Download: 10005x |
| 3. |
PCLinuxOS-2010 Download: 9500x |
| 4. |
alcolix Download: 12050x |
| 5. |
Onebase Linux Download: 10743x |
| 6. |
Novell Linux Desktop Download: 0x |
| 7. |
KateOS Download: 7189x |
| 1. |
xinetd Download: 3328x |
| 2. |
RDGS Download: 937x |
| 3. |
spkg Download: 6342x |
| 4. |
LinPacker Download: 11584x |
| 5. |
VFU File Manager Download: 3945x |
| 6. |
LeftHand Mała Księgowość Download: 8270x |
| 7. |
MISU pyFotoResize Download: 3653x |
| 8. |
Lefthand CRM Download: 4476x |
| 9. |
MetadataExtractor Download: 0x |
| 10. |
RCP100 Download: 4009x |
| 11. |
Predaj softveru Download: 0x |
| 12. |
MSH Free Autoresponder Download: 0x |
 linuxsoft.cz | Design:
www.megadesign.cz
linuxsoft.cz | Design:
www.megadesign.cz