
|
|
 Grafy a grafové algoritmy II
Grafy a grafové algoritmy II
Tento článek je zaměřen na hledání minimální kostry v grafu. V první části článku je teorie, která s minimální kostrou souvisí, v části druhé jsou vysvětleny dva algoritmy, které slouží k nalezení minimální kostry. Nechybí ani jejich implementace v jazyku C++.
15.2.2011 00:00 | Petr Sklenička | czytane 17271×
RELATED ARTICLES
KOMENTARZE
Úvod
Základní teorie, která se týká grafů, byla popsána v článku Grafy a grafové algoritmy I, proto se jí zde
nebudu dále zabývat. Pojmů a algoritmů, které souvisí s grafy, je však mnohem více než ve výše uvedeném článku.
Pojem, který bude v tomto článku stěžejní, je tzv. minimální kostra grafu. Dříve, než budeme formálně definovat
pojem kostry, musíme definovat pojem strom, neboť ten se právě objevuje v definici kostry.
Strom je souvislý jednoduchý graf, který neobsahuje kružnice.
O grafu, který neobsahuje kružnice, se říká, že je acyklický. To neznamená nic jiného, než že neobsahuje žádnou
smyčku (velmi jednoduše řečeno, nelze v něm chodit „pořád dokola“). Na následujícím obrázku je ukázka, jak
například může vypadat strom.
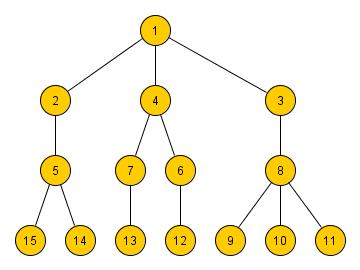
V souvislosti se stromy platí různé věty, pár jich uvádím.
- Strom, který má n vrcholů, má n – 1 hran (platí pro n > 0)
- Přidáme-li do stromu jednu novou hranu, tak vznikne graf s jednou kružnicí.
- Každý strom, který má více než jeden vrchol, má nějaký vrchol stupně jedna.
- Mezi každými dvěma vrcholy stromu lze nalézt právě jednu cestu.
Kostra grafu a minimální kostra grafu
Kostra souvislého grafu G je podgraf v G, přičemž je sám stromem a obsahuje všechny vrcholy grafu G.
Jinými slovy, kostra grafu obsahuje všechny vrcholy grafu, jehož kostru hledáme, ale pouze ty hrany, které poté ve
výsledku tvoří strom. Pro dokonalé pochopení uvádím obrázek grafu, společně s vyznačenou kostrou.
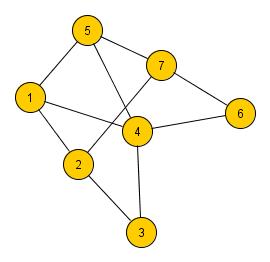
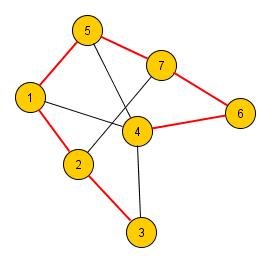
Kostra, která je na obrázku vyznačena, není jediná, kterou graf obsahuje, protože graf může mít mnohem více koster
než jednu. Důkaz, že se opravdu jedná o kostru, je snadný. Podgraf, který jsem vybral, obsahuje všechny vrcholy a
zároveň se jedná o strom. To, že je to opravdu strom, možná nemusí být někomu na první pohled patrné, ale je to
tak. Podgraf je souvislý, neobsahuje žádné kružnice, a věty, které jsem o stromech uváděl, pro něj také platí. Nyní
se konečně dostáváme k poslední definici, kterou je definice minimální kostry grafu.
Minimální kostra grafu je kostra, která má nejmenší ohodnocení.
Touto definicí jsme se dostali k váženým grafům, o kterých jsem psal v minulém článku. Na dalším obrázku uvádím
ohodnocený graf, společně s vyznačenou minimální kostrou.
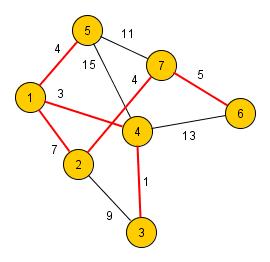
Na tomto obrázku si můžete všimnout, že graf je úplně stejný jako na předchozí ukázce, jen s tím rozdílem, že má
ohodnocené své hrany. Minimální kostra je vyznačena červenou barvou. Snad nemusím říkat, že minimální kostra je
jiná, než kostra, kterou jsem vyznačil na předchozím obrázku. Váha této kostry je 24 (součet vah jednotlivých hran
kostry). Skutečně se jedná o kostru minimální, neboť není možné najít kostru, která by měla menší váhu než 24.
Nyní se tedy nabízí hlavní otázka - jak minimální kostru najít? První způsob, jak to udělat, je využití Kruskalova
algoritmu.
Kruskalův algoritmus
Na pochopení je tento algoritmus poměrně jednoduchý. První krok tohoto algoritmu je seřazení všech hran grafu, dle
jejich vah (od nejmenší po největší). Celý postup si ukážeme na předchozím grafu. Náš graf má tedy 10 hran, přičemž
seřadíme-li jejich váhy od nejmenší po největší, dostaneme tuto posloupnost čísel:
1, 3, 4, 4, 5, 7, 9, 11, 13, 15
Poté budeme brát postupně jednotlivé hrany, a buď je přidáme do kostry, nebo ne. Kritérium pro rozhodování je
snadné – pokud právě přidávaná hrana nevytváří kružnici (neboli smyčku), přidáme ji. V opačném případě ji nepřidáme
a pokračujeme dále.
Nejprve tedy přidáme hranu s ohodnocením 1. Následuje hrana s ohodnocením 3. Tato hrana nám nemůže vytvořit
kružnici, proto ji můžeme také přidat do výsledné minimální kostry. Obdobným způsobem přidáváme hrany až do hrany s
ohodnocením 7. Následuje hrana s ohodnocením 9. Tu již ale nepřidáme – vytvořili bychom cyklus, což je v rozporu s
definicí kostry (cyklus by byl mezi vrcholy 1 – 2 – 3 – 4). Dále už nepřidáme žádnou hranu, neboť bychom opět
vytvořili nějaký cyklus. Prozkoumali jsme tedy všechny hrany, přičemž některé jsme přidali, jiné ne. Tím algoritmus
končí, neboť jsme získali minimální kostru grafu.
Implementace Kruskalova algoritmu
Při samotné implementaci je nejprve nutné zvolit vhodný způsob reprezentace grafu v počítači. V minulém článku jsme
používali matici sousednosti, která se ale pro Kruskalův algoritmus nehodí. Místo toho budeme graf reprezentovat
objekty tříd vrchol (Node) a hrana (Edge). Nebudu zde uvádět zdrojové kódy jednotlivých tříd, neboť celý zdrojový
kód je trochu delší a je možné si jej stáhnout níže. Každý vrchol má nějaké své ID, podle kterého jednoznačně
určíme, o jaký vrchol se jedná. Každá hrana obsahuje informace o tom, mezi kterými vrcholy vede a jaká je její
váha. To stačí k tomu, abychom věděli, o jaký graf se jedná.
Máme-li graf v počítači, není již těžké dát se do psaní samotného algoritmu. Problém může nastat snad jen při
zjišťování, zda hrana, kterou chceme přidat, bude nebo nebude tvořit cyklus. Tento problém lze poměrně snadno
vyřešit s pomocí tzv. Disjoint-setu. Jde o datovou strukturu a celé řešení problému je postaveno na základě
udržování reprezentantů komponent. V případě, že dva vrcholy mají stejného reprezentanta, patří tyto dva vrcholy do
stejné komponenty. Datová struktura Disjoint-set má dvě hlavní metody – Union a Find. První z uvedených metod má na
starost spojení dvou komponent, druhá slouží k nalezení reprezentanta. Nejčastěji se využívá n-ární strom a kořen
tohoto stromu je reprezentant. Metoda Find je tedy poměrně jednoduchá – z vrcholu, jehož reprezentanta hledáme,
stačí „stoupat nahoru“ tak dlouho, dokud nedojdeme ke kořeni. Pokud spojujeme dvě komponenty v jednu (metoda
Union), stačí menší podstrom zavěsit pod reprezentanta většího podstromu.
Celou ukázku implementace Kruskalova algoritmu v jazyce C++ je možné stáhnout zde. Myslím, že po přečtení si
způsobu, jak algoritmus funguje, a po prohlednutí kódu by měl být princip tohoto algoritmu poměrně jasný a proto
můžeme přejít na další algoritmus.
Jarníkův algoritmus
Tento algoritmus, stejně jako předchozí, slouží také k nalezení minimální kostry grafu. Jeho princip je však jiný,
proto si jej opět vysvětlíme na našem grafu.
Hned první změna oproti minulému algoritmu je v tom, že hrany nijak neseřazujeme. Místo toho si vybereme libovolný
vrchol, ve kterém začneme. Je úplně jedno, který vrchol zvolíme, neboť v kostře budou nakonec všechny vrcholy. Poté
se podíváme na všechny hrany, jež z tohoto vrcholu vedou, a vybereme tu s nejmenším ohodnocením. Ta bude součástí
výsledné kostry. Nyní máme tedy spojené dva vrcholy a opět hledáme hranu, která má nejmenší ohodnocení a vychází z
některého ze dvou vrcholů. Tuto hranu opět přidáme do kostry, čímž se dostaneme k dalšímu uzlu a celý postup
opakujeme. Zbývá jediná otázka – kdy skončit? Samozřejmě tehdy, až bude kostra úplná. To poznáme velmi jednoduše.
Stačí si uvědomit, že kostra grafu je strom a obsahuje všechny vrcholy grafu. My víme, že každý strom, který má n
vrcholů, má n – 1 hran. Čili například bude-li mít graf 20 vrcholů, jeho kostra bude mít 19 hran.
Abychom si celý tento postup ujasnili, najdeme minimální kostru grafu z ukázky. Vybereme tedy libovolný vrchol,
například vrchol 1. Z tohoto vrcholu vedou hrany, jejichž váhy jsou 7, 3 a 4. Nejmenší z nich je samozřejmě s váhou
3, proto tuto hranu přidáme do kostry. Díky tomu jsme se dostali do vrcholu 4 a nyní vybíráme jednu z celkem pěti
hran – dvě vedou ještě z vrcholu 1 a 3 z vrcholu 4. Je jasné, že vybereme hranu s ohodnocením 1. Díky ní se
dostáváme do vrcholu 3. Opět najdeme hranu s minimálním ohodnocením – to je hrana z vrcholu 1 do vrcholu 5, a její
váha je 4. Tímto způsobem postupujeme tak dlouho, dokud nevybereme 6 hran (graf má 7 vrcholů, kostra má tedy 7 – 1
hran).
Implementace Jarníkova algoritmu
V porovnání s implementací Kruskalova algoritmu je tato o něco snadnější. Graf nám bude stačit reprezentovat již známou maticí sousednosti, čímž nám tedy odpadají třídy Node a Edge. Také nám odpadá využití Disjoint-setu, který v minulém algoritmu sloužil jako kontrola, zda nevytváříme smyčku. Zde to bude jednodušší. Stačí si uvědomit, že tvoříme-li kostru tímto algoritmem, vždy v průběhu kreslení kostry máme souvislý graf, jinak řečeno, mezi všemi zatím přidanými uzly vede cesta. Díky tomuto postupu je možné cyklus vytvořit jedině tak, že bychom vedli hranu do vrcholu, který již je součástí kostry. A to je velmi snadné na ohlídání. Ukázka v jazyce C++ je k dispozici zde.
Závěr
Na závěr ještě zmíním, k čemu se vlastně nalezení minimální kostry grafu může hodit. Zkuste si například představit nějaké obce, vesnice, či města. Celé toto území chceme elektrifikovat. Můžeme tedy města převést na vrcholy, hrany nám budou reprezentovat elektrické spojení, přičemž ohodnocení hran bude znamenat cenu za natažení vedení. Minimální kostra tohoto grafu nám pak přesně určí, kudy vést vedení, abychom celý problém vyřešili nejlevněji.
C/C++ (1) - Úvod
C/C++ (2) - První program
C/C++ (3) - Proměnné a konstanty
C/C++ (4) - Funkce printf
C/C++ (5) - Funkce printf podruhé
C/C++ (6) - Operátory
C/C++ (7) - Podmínka
C/C++ (8) - Cykly
C/C++ (9) - Pole
C/C++ (10) - Standardní vstup a výstup
C/C++ (11) - Čtení a konverze čísel
C/C++ (12) - Preprocesor
C/C++ (13) - Preprocesor podruhé
C/C++ (14) - Funkce
C/C++ (15) - Proměnné
C/C++ (16) - Hlavičkové soubory
C/C++ (17) - Makefile
C/C++ (18) - Makefile podruhé
C/C++ (19) - Příkaz switch a bitové operátory
C/C++ (20) - Alokace paměti
C/C++ (21) - Práce s řetězci
C/C++ (22) - Struktury
C/C++ (23) - Seznam
C/C++ (24) - Soubory
C/C++ (25) - Funkce s proměnným počtem parametrů
C/C++ (26) - Standardní knihovna
C/C++ (27) - Standardní knihovna podruhé
C/C++ (28) - Standardní knihovna potřetí
C/C++ (29) - Standardní knihovna počtvrté
C/C++ (30) - Výčtový typ a nestandardní knihovny
C/C++ (31) - Jazyk C++, historie, charakteristika, vztah k C
C/C++ (32) - Omezení C++ oproti C
C/C++ (33) - Rozdíly mezi C a C++
C/C++ (34) - Drobná vylepšení C++
C/C++ (35) - Reference, funkce
C/C++ (36) - Prostory jmen
C/C++ (37) - Prostory jmen podruhé
C/C++ (38) - Prostory jmen potřetí
C/C++ (39) - Objektově orientované programování
C/C++ (40) - Dědičnost a virtuální metody
GCC vs. CLANG
C++ Binární vyhledávací stromy
C++ Datová struktura zásobník
C++ - Hashování
C++ - Vyhledávání v textu - Brute Force algoritmus
C++ šablony
Grafy a grafové algoritmy I
C++ výjimky
C++ Funktory neboli funkční objekty
Grafy a grafové algoritmy III.
C++ a garbage collector
Previous Show category (serial) Next
|
|
||
|
KOMENTARZE
Nie ma komentarzy dla tej pozycji. |
||
|
Tylko zarejestrowani użytkownicy mogą dopisywać komentarze.
|
||
| 1. |
Pacman linux Download: 5778x |
| 2. |
FreeBSD Download: 10005x |
| 3. |
PCLinuxOS-2010 Download: 9500x |
| 4. |
alcolix Download: 12050x |
| 5. |
Onebase Linux Download: 10742x |
| 6. |
Novell Linux Desktop Download: 0x |
| 7. |
KateOS Download: 7189x |
| 1. |
xinetd Download: 3328x |
| 2. |
RDGS Download: 937x |
| 3. |
spkg Download: 6342x |
| 4. |
LinPacker Download: 11584x |
| 5. |
VFU File Manager Download: 3945x |
| 6. |
LeftHand Mała Księgowość Download: 8270x |
| 7. |
MISU pyFotoResize Download: 3653x |
| 8. |
Lefthand CRM Download: 4475x |
| 9. |
MetadataExtractor Download: 0x |
| 10. |
RCP100 Download: 4009x |
| 11. |
Predaj softveru Download: 0x |
| 12. |
MSH Free Autoresponder Download: 0x |
 linuxsoft.cz | Design:
www.megadesign.cz
linuxsoft.cz | Design:
www.megadesign.cz